Physical Address
That’s it! Later we’ll talk about different reasons why something might be pushed or pulled, but at the end of the day, this definition will stay the same. Simply imagining forces as pushes and pulls will get you a long way.
Work, Power, and Energy
Work, Power and Energy is a very important concept in physics. Work done by all the forces is equal to the change in kinetic energy.
Contents
Work [ edit | edit source ]
In physics, work is related to the amount of energy transferred in or from a system by a force. It is a scalar-valued quantity with SI units of Joule.
Work can be represented in a number of ways. For the case where a body is moving in a steady direction, the work done by a constant force F acting parallel to the displacement Δ x is defined as
the dot product of force and displacement is known as work. W F = F ⋅ Δ x . =F~\cdot \Delta x\,\!.>
When the force is not acting parallel to the body’s direction of movement, the work done is defined as a dot product of the force and the displacement,
W F = F → ⋅ Δ x → = | | F → | | ⋅ | | Δ x → | | ⋅ cos ϕ . =>\cdot \Delta >=||>||\cdot ||\Delta >||\cdot \cos \phi \,\!.>
A few other ways of finding work can be either with the change of K for kinetic energy or the change of P for potential energy which can be resembled as:
Example [ edit | edit source ]
A wagon displaces by a distance of 2 m while under the influence of an 80 N force directed parallel to the motion. How much work is performed by the force exerted on the wagon?
W F = F Δ x = 80 N ⋅ 2 m = 160 N ⋅ m = 160 J o u l e s . =F\Delta x=80~>\cdot 2~>=160~>=160~>\,\!.>
Example [ edit | edit source ]
Suppose the same displacement of 2 m for the wagon while under the influence of an 80 N force 60 o to the axis of the motion. How much work is performed by the force exerted on the wagon in this case?
W F = F Δ x cos ( 60 ∘ ) = 80 N ⋅ 2 m ⋅ 0.5 = 80 N ⋅ m = 80 J o u l e s . =F\Delta x\cos(60^)=80~>\cdot 2~>\cdot 0.5=80~>=80~>\,\!.> and dimensions of work is equal to the energy
Power [ edit | edit source ]
Power is defined to be the rate at which work is performed, or the derivative of work over time. The SI unit for power is the watt. OR: Rate of doing work with respect to time is called power
Average power is the average amount of work done per unit of time. Thus instantaneous power is the limiting power of the average power as Δt approaches zero.
When the work is done steadily (constant power), just use P = W/t. That is, the power is the work done divided by the time taken to do it.
Example: A garage hoist steadily lifts a car up 2 meters in 15 seconds. Calculate the power delivered to the car. Use 1000 kg for the mass of the car.
First we need the work done, which requires the force necessary to lift the car against gravity:
F = mg = 1000 x 9.81 = 9810 N.
W = Fd = 9810N x 2m = 19620 Nm = 19620 J.
The power is P = W/t = 19620J / 15s = 1308 J/s = 1308 W. P=f.v
Energy [ edit | edit source ]
Energy is stored work. It has the same units as work, the Joule (J).
There are many forms of energy:
Spring energy: Work has been done on a spring to compress or stretch it; the spring has the ability to push or pull on another object and do work on it. The force required to stretch a spring is proportional to the distance it is stretched: F = kx where x is the stretch distance and k is a constant characteristic of the spring (big heavy springs have larger k values). The work done in stretching a spring from 0 to x is the integral of dW = Fdx. Since the force function is linear, we can just take the average force of kx/2 and avoid using calculus:
W = average F x distance = (kx/2)(x) = ½kx²
Assuming 100% efficiency, the energy stored in a stretched spring is the same as the work done in stretching it, so Spring E = ½kx²
Example: How much energy is stored in a spring with k = 2000 N/m that has been stretched 1 cm away from its equilibrium length?
E = ½kx² = ½(2000)(0.01)² = 0.1 J
Gravitational potential energy: a mass has been lifted to a height; when released it will be pulled down by gravity and can do work on another object as it falls.
Example: Find the energy stored in a tonne of water at the top of a 20 m high hydroelectric dam.
The long way is to use F = mg and then W = Fd to find the work needed to lift the water up.
The short way is to combine the formulas, replacing F with mg and using h (height) in place of d:
Gravitational energy = W = Fd = mgh
Egravity = mgh = (1000 kg)(9.81 m/s²)(20 m) = 196200 kg m²/s² = 1.96 x 10 5 J
Kinetic energy: A mass is moving and can do work when it hits another object. Ekinetic = ½mΔV 2 = ½m(Vf 2 -Vi 2 )
Example: A 8kg ball is moving at 5m/s. EK = ½(8 kg)(5 m/s) 2 = 100 J.
Electrical energy: Electrons can flow out of a battery or capacitor and do work on another electrical component such as a light bulb.
Photon energy: Although massless, a photon does have energy; in the amount hf where f is the photon’s frequency and h is Planck’s constant. This is the energy that warms your face in the morning sun and burns your unguarded nose at the beach.
Example: Red, at 400Thz has energy
Ered = hf = (6.626×10−34
J⋅s)(400×10+12
hz) = 2.5e-19 J
Not much from each photon, but photons come from the sun in vast numbers; one estimate is 10 17 photons per second per square centimeter.
Chemical energy: When some kinds of molecules are combined with others, energy can be released, usually as heat, light, or motion. When coal is burned it releases photon energy stored by plants millions of years before. When hydrogen combines with oxygen to form water, heat is released as well. A fire is oxygen combining with other substances; this also produces heat. Mixing mentos and coke produces foam whose mechanical properties can be exploited as in a MythBuster’s Christmas machine.
Example: One stick of dynamite produces about a Megajoule.
Nuclear energy: When an atom fissions it releases various particles and a little bit of heat. This energy was stored when the atom was created in the depths of a nova, an exploding star. Although the heat from each fission is miniscule, when the released particles trigger a cascade of fissioning atoms, the total energy can be enormous; as evidenced by the destruction wrought by an atomic weapon.
Example: The heat from splitting one Uranium atom is 6.9e-13 J.
Force, Work, and, Energy for the MCAT: Everything You Need to Know
Learn key MCAT concepts about work, energy, and force, plus practice questions and answers

(Note: This guide is part of our MCAT Physics series .)
Part 1: Introduction to forces, energy, and work
Part 2: Forces
a) Types of forces
b) Newton’s three laws
c) Conservative versus nonconservative forces
Part 3: Energy
a) Types of energy
b) Conservation of energy
Part 4: Work
a) Work done by constant force
b) Work-kinetic energy theorem
c) Power
d) Mechanical advantage
e) Torque
Part 5: High-yield terms and equations
Part 6: Practice passage on force, work, and energy
Part 7: Force, work, and energy practice questions
Part 1: Introduction to forces, energy, and work
Forces, energy, and work are some of the first subjects taught in most introductory physics classes. While these are only medium-yield MCAT subjects, understanding them can help with much more than force and energy-specific questions. They’re super important for most other physics topics, and they might even help you develop an intuition for some concepts in biology or chemistry!
In the guide below, you’ll find the most important terms in bold font. When you see one, try to define it in your own words and create your own examples. This is a great way to check your understanding, and studying will be much easier in the long run if you phrase things in a way that makes the most sense to you!
At the end of this guide, there’s an MCAT-style practice passage and standalone questions that will not only test your knowledge on forces, energy, and work but also show you how the AAMC likes to ask questions.
Let’s get started!
Part 2: Forces
“Force” is a word you’ve probably heard before in a number of ways, but its definition in physics is more precise:
A force is a push or pull that makes something accelerate if it is unopposed.
That’s it! Later we’ll talk about different reasons why something might be pushed or pulled, but at the end of the day, this definition will stay the same. Simply imagining forces as pushes and pulls will get you a long way.
Forces are also vectors, which mean that they have both magnitude and direction. Every force must have both. To think about vectors, imagine an arrow similar to the ones shown below.
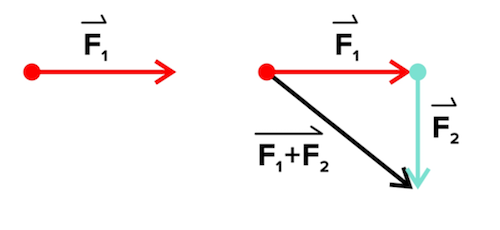
An arrow has to have some length, and it has to point in some direction; otherwise, it’s not an arrow. Like all vectors, forces can also be combined. Forces in the same direction will make a bigger force, and forces in opposite directions will cancel out.
The last thing you should know about forces is also important: the unit of measurement for forces is Newtons.
Now that we’ve gone over the basics, let’s look at some different types of forces.
a) Types of forces
Imagine you throw a football and kick a soccer ball shortly afterwards. The magnitude of each force will depend on different properties, specifically the strength of your arm muscles versus your leg muscles. In the same way, the universe has different kinds of “muscles” that come up a lot in physics problems. Let’s talk about two of the most common ones.
Gravitational Force: This is the force that pulls masses toward each other. You remember it from all those times you jumped in the air and didn’t fly off into space! There is a general equation for the gravitational force between any two objects in the universe, but when you’re on earth, the equation simplifies to the following:
Fg = m * g
where Fg = the force on the object due to gravity, m = the mass of the object, and = 9.8 m/s 2 , the acceleration due to gravity
The force of gravity on an object is also called that object’s weight. People often think weight and mass are the same, but they actually aren’t. Here’s a definition for each:
Mass: the amount of matter in something, measured in kilograms.
Weight: the strength of the gravitational force on something, measured in Newtons.
To get from mass to weight for an object on earth, multiply by 9.8. So, if a backpack has a mass of 10 kg, it weighs 98 N.
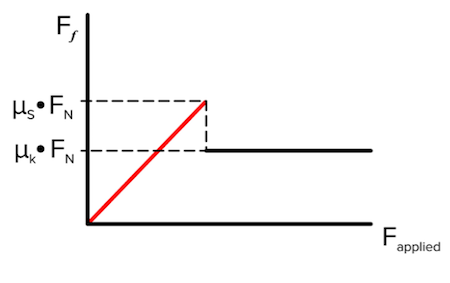
Friction: This is the force that tries to slow down an object sliding across a surface. To find the magnitude of friction, you use the following equation:
f = FN * μ
where f = the force of friction, FN = the normal force, and μ = the coefficient of friction.
(A normal force is the force that a surface pushes on the object with. It is called “normal” because in physics “normal” is a synonym for “perpendicular,” and surfaces always push objects in a perpendicular direction. On a horizontal surface, the normal force is equal to the object’s weight.)
There are two more important things to remember about friction:
1. Friction is a non-conservative force. We’ll talk about this more later, but it essentially means that friction sucks energy out of the system.
2. The coefficient of friction depends on the materials involved and whether or not the object is moving. The coefficient of static friction is used when the object is at rest. It gives the maximum force that friction can resist with before the object begins to move. Once the object is moving, the coefficient of kinetic friction takes over. It gives a weaker constant force that resists movement.
Instead of calculating forces working on every single particle within an object, it is sufficient to consider the force as acting on a single point. To simplify calculations, a force is considered to work on the center of mass of an object. The center of mass is a single point inside an object that represents the weighted average location of the mass distribution.
Every type of force has its own rules, but this means you’ll often be given these equations if you need them in a problem. The following rules are true for all forces, and it’s more likely that you’ll have to remember them on your own.
b) Newton’s three laws
These three laws are true for all forces; Newton’s laws tell you what the forces we talked about earlier do. Here’s what each says:
1. Newton’s First Law: An object at rest will stay at rest unless a force acts on it, and an object in motion will stay in motion unless a force acts on it.
The first law is the reason you’d fly off a bike if you ride into a curb: you’re moving, and the curb only applies a force to the bike, so you keep on moving, right onto the (hopefully) grass.
2. Newton’s Second Law: The summation of forces on an object is equal to the mass of the object times its acceleration.
This is the most important of Newton’s Laws, and one of the most important laws in physics. It usually appears as
ΣF = m*a
where ΣF = the net force, m = the mass of the object, and a = the acceleration of the object.
The second law is very important, so let’s go through each term in that equation.
ΣF: the net force, or the one leftover after you combine all the initial forces. This reminds us that we have to consider every force acting on an object before we can say for sure whether it’s accelerating. It opens the door for combining forces or for forces to cancel out. To help sort through all the different forces, we often draw free-body diagrams, which are shown below.









